深入了解递归

正所谓人理解迭代，神理解递归，今天我们来总结递归。递归很容易和树结合在一起考察。

写递归算法的注意事项：

以前我写递归很容易先把自己递进去，人脑 debug 一遍，有的时候能归出去，有的时候很容易就把自己给绕进去了。

后来学聪明点了：写树相关的题目，先搞明白当前的 root 节点该干什么，然后根据任务要求递归调用子节点，递归调用会让孩子节点做相同的事情。例如：

翻转二叉树

// 将整棵树的节点翻转
TreeNode invertTree(TreeNode root) {
    // base case
    if (root == null) {
        return null;
    }

    /**** 前序遍历位置 ****/
    // root 节点需要交换它的左右子节点
    TreeNode tmp = root.left;
    root.left = root.right;
    root.right = tmp;
	// 每一层调用 root 就把它的左右孩子指针交换一下就行
    
    // 让左右子节点继续翻转它们的子节点
    invertTree(root.left);
    invertTree(root.right);

    return root;
}

注意交换逻辑可以放到前序遍历的位置（从上到下）、也可以放到后序遍历的位置（从下到上），但是你不能放到中序遍历的位置上：因为你递归递到最左边的叶子节点，交换了它的父节点的左右孩子，又接着执行 invertTree(root.right); ，现在的 root.right 可是保存的 root.left 的信息（交换了嘛！）

这道题想要告诉我二叉树题目的一个难点就是，如何把题目的要求细化成每个节点需要做的事情。

填充每个节点的下一个右侧节点指针

class Solution {
private:
    void traversal(Node* cur) {
        if (cur == NULL) return;
                                // 中
        if (cur->left) cur->left->next = cur->right; // 操作1
        if (cur->right) {
            if (cur->next) cur->right->next = cur->next->left; // 操作2 
            else cur->right->next = NULL;
        }
        traversal(cur->left);   // 左
        traversal(cur->right);  // 右
    }
public:
    Node* connect(Node* root) {
        traversal(root);
        return root;
    }
};

作者：carlsun-2
链接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/solution/116-di-gui-yu-die-dai-xiang-jie-by-carlsun-2/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

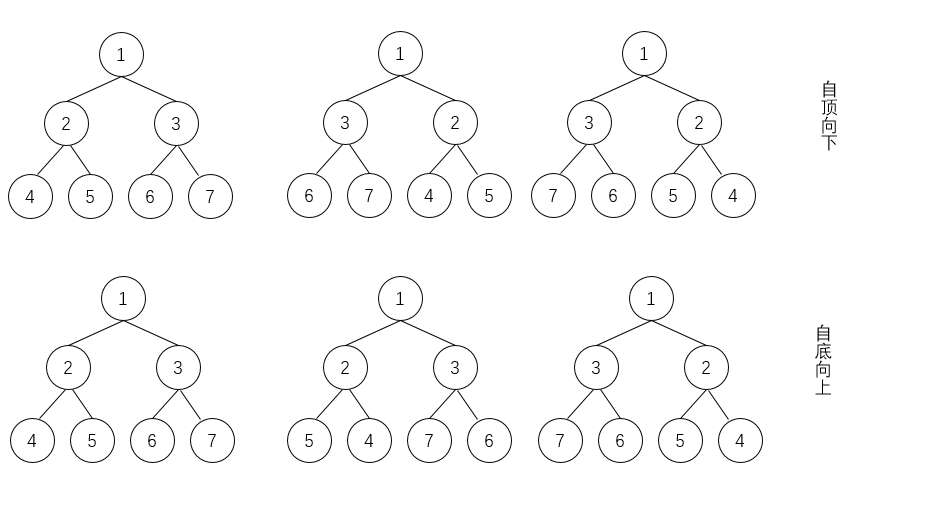
镜像二叉树

这道题我一开始想的是前序遍历那种方式：先交换 root 的左右孩子，接着递归下去；也就是传说的自顶向下，可以这样理解

【1，2，3，4， 5， 6， 7】

​

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if (root == nullptr) return nullptr;
        TreeNode* tmp = root->left;
        root->left = root->right;
        root->right = tmp;
        mirrorTree(root->left);
        mirrorTree(root->right);
        return root;
    }
};

看了别人的解法是自底向上的

public TreeNode mirrorTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        TreeNode leftRoot = mirrorTree(root.right);
        TreeNode rightRoot = mirrorTree(root.left);
        root.left = leftRoot;
        root.right = rightRoot;
        return root;
    }

对称二叉树

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

首先明确是自底向上还是自顶向下？

应该是自顶向下吧

先比较 root 的左孩子和右孩子

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return root == nullptr? true : (recur(root->left, root->right));
    }
    bool recur(TreeNode* l, TreeNode* r) {
        if (l == nullptr && r == nullptr) return true;
        if (l == nullptr || r == nullptr || l->val != r->val) {
            return false;
        }
        return recur(l->left, r->right) && recur(l->right, r->left);
    }
};

二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

int minDepth(TreeNode* root) {
        if(root == NULL) return 0;  //空树深度为0
        if(root -> left == NULL && root -> right == NULL) return 1; //左右子树为空，深度为1
        //根据题意，若一颗子树为空，则最小深度为非空子树的最小深度加一
        if(root -> left == NULL && root -> right != NULL) return minDepth(root -> right) + 1;
        if(root -> left != NULL && root -> right == NULL) return minDepth(root -> left) + 1;
        //若两颗子树都非空，则最小深度为左右子树最小深度较小者加一
        return min(minDepth(root -> left), minDepth(root -> right)) + 1;
    }

判断二叉搜索树

判断平衡二叉树

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

isBalanced(root->left) && isBalanced(root->right);是用来判断直链情况的

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root == nullptr) return true;
        return abs(depth(root->left) - depth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
    int depth(TreeNode* root){
        if(root == nullptr) return 0;
        return max(depth(root->left), depth(root->right)) + 1;
    }
};

单值二叉树

class Solution {
public:
    bool isUnivalTree(TreeNode* root) {
        return isUnivalTree(root, root->val);
    }
    bool isUnivalTree(TreeNode* root, int val){
        if(!root) return 1;
        if(root->val != val) return 0;
        return isUnivalTree(root->left, root->val) && isUnivalTree(root->right, root->val);
    }
};

二叉树的直径

二叉树的直径就是求左子树的最长深度加上右子树的最长深度

https://leetcode-cn.com/problems/diameter-of-binary-tree/solution/shi-pin-jie-shi-di-gui-dai-ma-de-yun-xing-guo-chen/

class Solution {
    int ans;
    int depth(TreeNode* rt){
        if (rt == NULL) return 0; // 访问到空节点了，返回0
        int L = depth(rt->left); // 左儿子为根的子树的深度
        int R = depth(rt->right); // 右儿子为根的子树的深度
        ans = max(ans, L + R + 1); // 计算d_node即L+R+1 并更新ans
        return max(L, R) + 1; // 返回该节点为根的子树的深度
    }
public:
    int diameterOfBinaryTree(TreeNode* root) {
        ans = 1;
        depth(root);
        return ans - 1;
    }
};

二叉树的非递归后序遍历

要保证根结点在左孩子和右孩子访问之后才能访问，因此对于任一结点P，先将其入栈。如果P不存在左孩子和右孩子，则可以直接访问它；或者P存在左孩子或者右孩子，但是其左孩子和右孩子都已被访问过了，则同样可以直接访问该结点。若非上述两种情况，则将P的右孩子和左孩子依次入栈，这样就保证了每次取栈顶元素的时候，左孩子在右孩子前面被访问，左孩子和右孩子都在根结点前面被访问。

-----前序
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                st.push(node);                          // 中
                st.push(NULL);
            } else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};
-----中序
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node->right) st.push(node->right); // 添加右节点

                st.push(node); // 添加中节点
                st.push(NULL); // 中节点访问过，但是还没有处理，需要做一下标记。

                if (node->left) st.push(node->left); // 添加左节点
            } else {
                st.pop(); // 将空节点弹出
                node = st.top(); // 重新取出栈中元素
                st.pop();
                result.push_back(node->val); // 加入到数组中
            }
        }
        return result;
    }
};
-----后序
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);

                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左

            } else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};
class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        if (root == nullptr) {
            return res;
        }

        stack<TreeNode *> stk;
        TreeNode *prev = nullptr;
        while (root != nullptr || !stk.empty()) {
            while (root != nullptr) {
                stk.emplace(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            if (root->right == nullptr || root->right == prev) {
                res.emplace_back(root->val);
                prev = root;
                root = nullptr;
            } else {
                stk.emplace(root);
                root = root->right;
            }
        }
        return res;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/er-cha-shu-de-hou-xu-bian-li-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

打家劫舍3 很巧妙

class Solution {
public:
    unordered_map <TreeNode*, int> f, g;

    void dfs(TreeNode* o) {
        if (!o) {
            return;
        }
        dfs(o->left);
        dfs(o->right);
        f[o] = o->val + g[o->left] + g[o->right];
        g[o] = max(f[o->left], g[o->left]) + max(f[o->right], g[o->right]);
    }

    int rob(TreeNode* o) {
        dfs(o);
        return max(f[o], g[o]);
    }
};

完全二叉树的节点个数

看到大佬写的程序感觉自愧不如：这段代码值得天天阅读，啥时候我也能写出这种程序来就好了

https://leetcode-cn.com/problems/count-complete-tree-nodes/solution/er-fen-cha-zhao-wei-yun-suan-by-docker-a-u9ui/

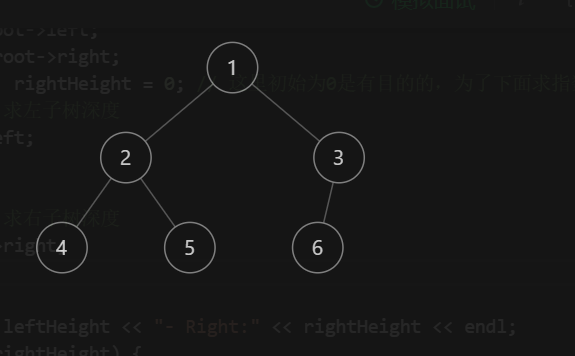
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr) return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftHeight = 0, rightHeight = 0; // 这里初始为0是有目的的，为了下面求指数方便
        while (left) {  // 求左子树深度
            left = left->left;
            leftHeight++;
        }
        while (right) { // 求右子树深度
            right = right->right;
            rightHeight++;
        }
        if (leftHeight == rightHeight) {
            return (2 << leftHeight) - 1; // 注意(2<<1) 相当于2^2，所以leftHeight初始为0
        }
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

left:2- Right:1

left:1- Right:1

left:1- Right:0

left:0- Right:0

先开始，root = 1,进来left->2->4 为 2，right->3->null为 1，左右不等 进入 return countNode(&2) + countNode(&3) + 1;

执行 countNode(&2) 函数，left->4为 1，right->5为1，左右等，返回2*2 - 1 = 3 至 countNode(&2) 帧

再执行 countNode(&3) 函数，left->6 为 1，right->null 为 0 ，左右不等，进入 return countNode(&6) + countNode(&null) + 1;

再执行 countNode(&6) 函数，left 和 right 都为 0，返回 1 至 countNode(&6) 帧

由于countNode(&null) 返回 0 所以 return countNode(&6) + countNode(&null) + 1;返回 2 至 return countNode(&2) + countNode(&3) + 1;

由此 返回 3 ＋ 2 + 1 = 6

二叉树的最近公共祖先

这里将每个节点的父亲节点保存在哈希表里，从p 开始往上进行遍历，遍历过的节点置1

然后从 q 也往上遍历， 直到找到遍历过的节点

这里需要注意一个东西：

dfs 里递归时是两个 if ，如果第二个 if 换成 else if ,那么递归到左子树叶子节点后它就不会继续返回上层去遍历右子树去了，和上一小节的描述是相似的。以后一定要考虑好是用 if 还是 else if

class Solution {
public:
    unordered_map<int, TreeNode*> fa;
    unordered_map<int, bool> vis;
    void dfs(TreeNode* root) {
        if (root->left) {
            fa[root->left->val] = root;
            dfs(root->left);
        }
        if (root->right) {
            fa[root->right->val] = root;
            dfs(root->right);
        }
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        fa[root->val] = nullptr;
        dfs(root);
        while (p) {
            vis[p->val] = true;
            p = fa[p->val];
        }    
        while (q) {
            if (vis[q->val]) return q;
            q = fa[q->val];
        }
        return nullptr;
    }
};

二叉搜索树第K大

这道题可有讲究了：题目要求的是第K大；所以是从右子树开始遍历的；同时在遍历到0之后需要退出，不执行之后所有的递归调用了

class Solution {
public:
    int k;
    int res;
    int kthLargest(TreeNode* root, int k_) {
        k = k_;
        dfs(root);
        return res;
    }
    void dfs(TreeNode* root) {
        if(root == nullptr) return;
        dfs(root->right);
        if(k == 0) return;
        if(--k == 0) res = root->val;
        dfs(root->left);
    }
};

判断完全二叉树

class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        queue<TreeNode*>q;
        q.push(root);
        bool flag=false;
        while(!q.empty()){
            auto node =q.front();
            q.pop();
            if(node==nullptr){
                flag=true;
                continue;
            }
            if(flag) return false;
            q.push(node->left);
            q.push(node->right);
            
        }
        return true;
    }
};
----------------
    bool isCompleteTree(TreeNode* root) {
    queue<pair<TreeNode*, int>> q;
    int prev = 1;
    q.emplace(make_pair(root, 1));
    while(!q.empty()) {
        auto front = q.front();
        if(prev != front.second) return false; 
        q.pop();
        prev = front.second +1;
        if(front.first) {
            if(front.first->left) q.emplace(make_pair(front.first->left, front.second *2));
            if(front.first->right) q.emplace(make_pair(front.first->right, front.second *2 +1));
        }
    }
    return true;
}