数据结构 | acewzj

本文主要关于数据结构，数据结构是指数据存储的组织方式。大致上分为线性表、栈（Stack）、队列、树（tree）、图（Map）。

具体涉及算法如下：

dfs

463.岛屿的周长

695.岛屿的最大面积

200.岛屿的数量

class Solution {
private:
    void dfs(vector<vector<char>>& grid, int r, int c) {
        int nr = grid.size();
        int nc = grid[0].size();

        grid[r][c] = '0';
        if (r - 1 >= 0 && grid[r-1][c] == '1') dfs(grid, r - 1, c);
        if (r + 1 < nr && grid[r+1][c] == '1') dfs(grid, r + 1, c);
        if (c - 1 >= 0 && grid[r][c-1] == '1') dfs(grid, r, c - 1);
        if (c + 1 < nc && grid[r][c+1] == '1') dfs(grid, r, c + 1);
    }

public:
    int numIslands(vector<vector<char>>& grid) {
        int nr = grid.size();
        if (!nr) return 0;
        int nc = grid[0].size();

        int num_islands = 0;
        for (int r = 0; r < nr; ++r) {
            for (int c = 0; c < nc; ++c) {
                if (grid[r][c] == '1') {
                    ++num_islands;
                    dfs(grid, r, c);
                }
            }
        }

        return num_islands;
    }
};

694.不同岛屿的数量

305.岛屿数量II

773. 滑动谜题

链表

24. 两两交换链表中的节点

25. K 个一组翻转链表

92. 反转链表 II

160. 相交链表

2.两数之和

剑指 Offer 24. 反转链表

面试题 02.05. 链表求和
动态规划
- 背包问题
```
*手撕0-1背包*

*416.分割等和子集*

*518.零钱兑换 II*

*70. 爬楼梯*

*322. 零钱兑换*
```
  - 博弈论
    
    877. 石子游戏
  - 贪心
    
    柠檬找零
  - 其他
    
    312. 戳气球
    
    剑指 Offer 14- I. 剪绳子
    
    剑指 Offer 14- II. 剪绳子 I
    
    42.接雨水
    
    860. 柠檬水找零
    
    72. 编辑距离
二分

排序数组，平方后，数组当中有多少不同的数字（相同算一个）

一个数据先递增再递减，找出数组不重复的个数，比如 [1, 3, 9, 1]，结果为3，不能使用额外空间，复杂度o(n)

递增数组，找出和为k的数对

给出一个数组nums，一个值k，找出数组中的两个下标 i，j 使得 nums[i] + nums[j] = k
滑动窗口

3.无重复字符的最长子串

字符串的排列
排序

插入排序

冒泡排序

快速排序

三路快排

归并排序
sum问题

两数之和

三数之和

nSum

大数之和
栈

71.简化路径
哈希表及Union-Find

128.最长连续序列

一个无序数组，从小到大找到第一个缺的数，比如[8 2 4 3 6 9 7 11 12],第一个缺的就是5

31.下一个排列

55.跳跃游戏

AB两个排序数组，原地合并数组。（A当中穿插一些无效数字怎么处理？)
树

手撕二叉树操作

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

剑指 Offer 68 - II. 二叉树的最近公共祖先

337. 打家劫舍 III

100.相同的树

前中后非递归遍历及递归遍历

剑指 Offer 54. 二叉搜索树的第k大节点

222. 完全二叉树的节点个数

257. 二叉树的所有路径

129. 求根到叶子节点数字之和

最小路径和

124. 二叉树中的最大路径和

112.路径总和

113.路径总和 II

剑指 Offer 07. 重建二叉树
手撕算法相关

手撕lru

手撕memcpy、strcpy、strnpy、strlen、strstr、strcat、strcmp

手撕智能指针

手撕kmp

手撕单例

手撕堆
- 手撕两种线程安全的单例模式
  - scoped_ptr
  - autpo_ptr
  - unique_ptr
  - shared_ptr

首先看一下什么是排列，什么是组合？

排列和组合的本质区别是：决策的顺序对结果有没有影响？

你一听排列，首先想到的就是排队，你站队头和站队尾那是两种排列；

例如 3 2 1 和 1 2 3 是两种排列

3！*2！ *1！

而组合对顺序无感，所以你站队头站队尾都是一种组合；

例如 3 2 1 和 1 2 3 是一种组合

(3！* 2！ * 1！) / (3 * 2)

“排列”类型问题和“子集、组合”问题不同在于：“排列”问题使用used数组来标识选择列表，而“子集、组合”问题则使用start参数

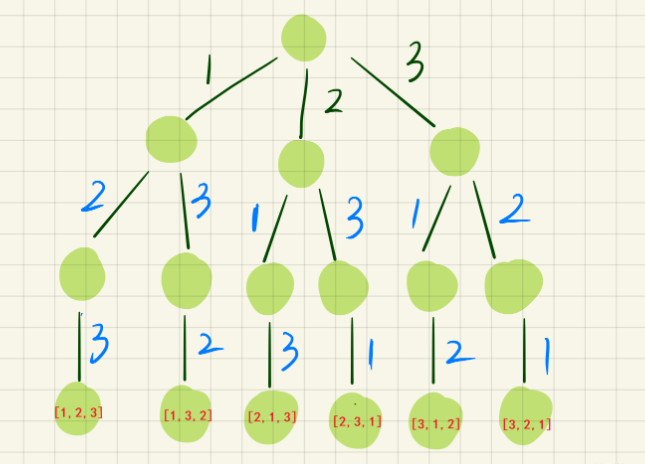
排列类问题

给定一个没有重复数字的序列，返回其所有可能的全排列。
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

首先，我们固定1，然后只有2、3可选：如果选2，那就只剩3可选，得出结果[1,2,3]；如果选3，那就只剩2可选，得出结果[1,3,2]。再来，如果固定2，那么只有1,3可选：如果选1，那就只剩3，得出结果[2,1,3]…..
有没有发现一个规律：如果我们固定了(选择了)某个数，那么他的下一层的选择列表就是——除去这个数以外的其他数。比如，第一次选择了2，那么他的下一层的选择列表只有1和3；如果选择了3，那么他的下一层的选择列表只有1和2,那么这个时候就要引入一个used数组来记录使用过的数字。

void backtrack(vector<int>& nums,vector<bool>&used,vector<int>& path)//used初始化为false
{
    if(path.size()==nums.size())
    {
        res.push_back(path);
        return;
    }
    for(int i=0;i<nums.size();i++)//从给定的数中除去，用过的数，就是当前的选择列表
    {
        if(!used[i])//如果没用过
        {
            path.push_back(nums[i]);//做选择
            used[i]=true;//设置当前数已用
            backtrack(nums,used,path);//进入下一层
            used[i]=false;//撤销选择
            path.pop_back();//撤销选择
        }
    }

}

作者：show-me-the-code-2
链接：https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/solution/c-zong-jie-liao-hui-su-wen-ti-lei-xing-dai-ni-ga-4/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

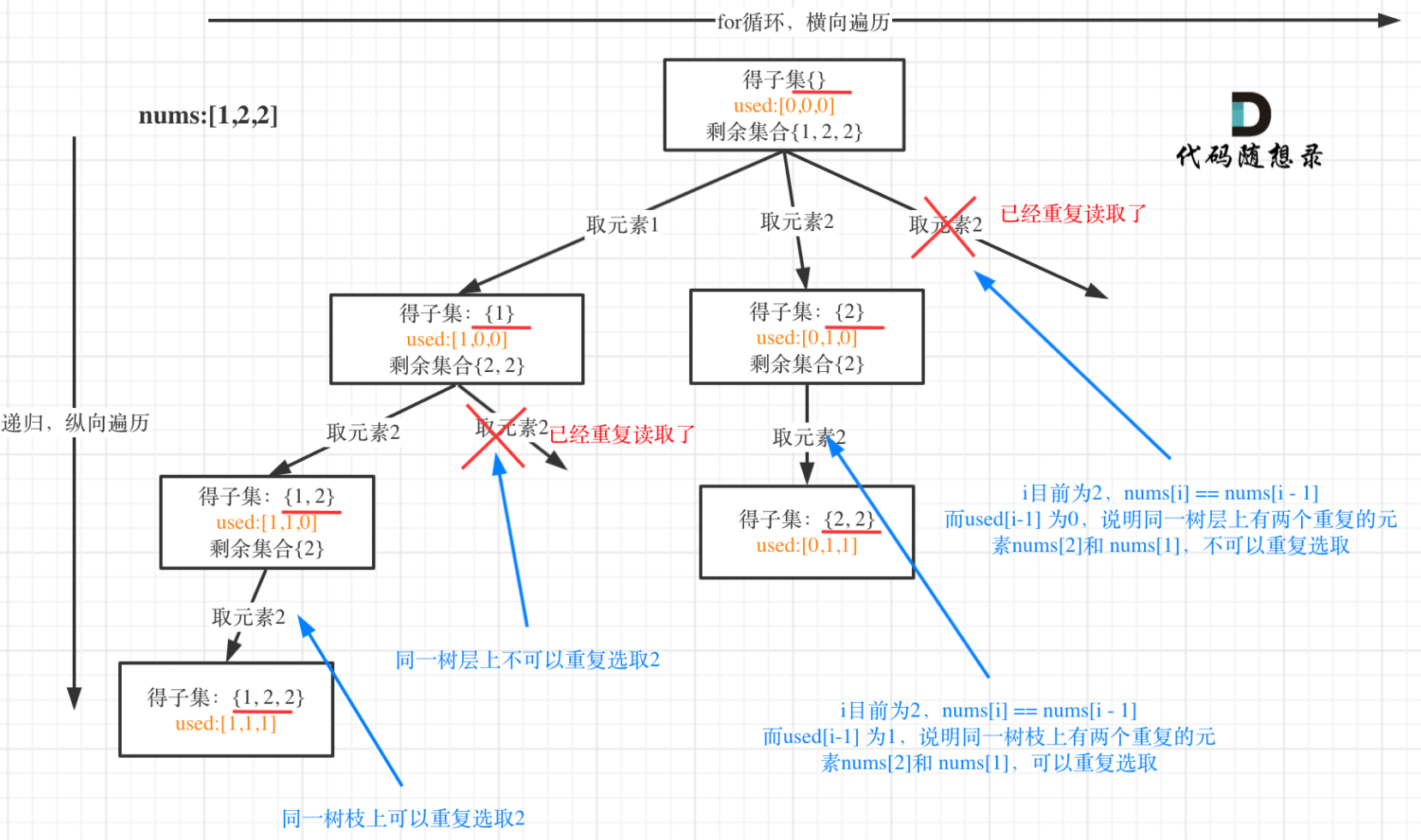
给定一个可包含重复数字的序列，返回所有不重复的全排列。
输入: [1,2,2]
输出:
[
[1,2,2],
[2,1,2],
[2,2,1]
]

有了前面“子集、组合”问题的判重经验，同样首先要对题目中给出的nums数组排序，让重复的元素并列排在一起，在

if(i>start&&nums[i] == nums[i-1])，基础上修改为if(i>0&&nums[i]==nums[i-1]&&!used[i-1])，语义为：当i可以选第一个元素之后的元素时(因为如果i=0，即只有一个元素，哪来的重复？有重复即说明起码有两个元素或以上,i>0)，然后判断当前元素是否和上一个元素相同？如果相同，再判断上一个元素是否能用？如果三个条件都满足，那么该分支一定是重复的，应该剪去

void backtrack(vector<int>& nums,vector<bool>&used,vector<int>& path)//used初始化全为false
{
    if(path.size()==nums.size())
    {
        res.push_back(path);
        return;
    }
    for(int i=0;i<nums.size();i++)//从给定的数中除去，用过的数，就是当前的选择列表
    {
        if(!used[i])
        {
            if(i>0&&nums[i]==nums[i-1]&&!used[i-1])//剪枝，三个条件
                continue;
            path.push_back(nums[i]);//做选择
            used[i]=true;//设置当前数已用
            backtrack(nums,used,path);//进入下一层
            used[i]=false;//撤销选择
            path.pop_back();//撤销选择
        }
    }
}

作者：show-me-the-code-2
链接：https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/solution/c-zong-jie-liao-hui-su-wen-ti-lei-xing-dai-ni-ga-4/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

组合类问题

正好最近在担任组合数学的助教，刷的题目很多都跟组合有关。遂总结一下：

77.给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

class Solution {
private:
    vector<vector<int>> result; // 存放符合条件结果的集合
    vector<int> path; // 用来存放符合条件结果
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        // 这个for循环有讲究，组合的时候 要用startIndex，排列的时候就要从0开始
        for (int i = startIndex; i <= n; i++) {//这个for是横向进行遍历
            path.push_back(i); // 处理节点 
            backtracking(n, k, i + 1);//这里是纵向进行dfs
            path.pop_back(); // 回溯，撤销处理的节点，这里是假如你找了两个，到了叶子节点，你需要回退成上一个状态
        }
    }
public:

    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

剪枝优化

在遍历的过程中如下代码：

for (int i = startIndex; i <= n; i++)
这个遍历的范围是可以剪枝优化的，怎么优化呢？

来举一个例子，n = 4， k = 4的话，那么从2开始的遍历都没有意义了。

已经选择的元素个数：path.size();

要选择的元素个数 : k - path.size();

在集合n中开始选择的起始位置 : n - (k - path.size());

因为起始位置是从1开始的，而且代码里是n <= 起始位置，所以集合n中开始选择的起始位置 : n - (k - path.size()) + 1;

所以优化之后是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)

39.给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
[7],
[2,2,3]
]

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum > target) {
            return;
        }
        if (sum == target) {
            result.push_back(path);
            return;
        }

        // 这里i 依然从 startIndex开始，因为求的是组合，如果求的是排列，那么i每次都从0开始
        for (int i = startIndex; i < candidates.size(); i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i); // 关键点在这里，不用i+1了，表示可以重复读取当前的数
            sum -= candidates[i];
            path.pop_back();

        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

手写：子集

很多同学在去重的问题上想不明白，其实很多题解也没有讲清楚，反正代码是能过的，感觉是那么回事，稀里糊涂的先把题目过了。

这个去重为什么很难理解呢，所谓去重，其实就是使用过的元素不能重复选取。这么一说好像很简单！

都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。

那么问题来了，我们是要同一树层上使用过，还是统一树枝上使用过呢？

回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。

所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

剧透一下，后期要讲解的排列问题里去重也是这个套路，所以理解“树层去重”和“树枝去重”非常重要。

用示例中的[1, 2, 2] 来举例，如图所示：（注意去重需要先对集合排序）

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtrack(vector<int>& nums, vector<bool>& used, int startIndex) {
        result.push_back(path);
        for (int i = startIndex; i < nums.size(); ++i) {
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            path.push_back(nums[i]);
            used[i] = true;
            backtrack(nums, used, i + 1);
            used[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        path.clear();
        result.clear();
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end());
        backtrack(nums, used, 0);
        return result;
    }
};

从先序遍历还原二叉树

class Solution {
public:
    TreeNode* recoverFromPreorder(string S) {
        stack<TreeNode*> path;
        int pos = 0;
        while (pos < S.size()) {
            int level = 0;
            while (S[pos] == '-') {
                ++level;
                ++pos;
            }
            int value = 0;
            while (pos < S.size() && isdigit(S[pos])) {
                value = value * 10 + (S[pos] - '0');
                ++pos;
            }
            TreeNode* node = new TreeNode(value);
            if (level == path.size()) {
                if (!path.empty()) {
                    path.top()->left = node;
                }
            }
            else {
                while (level != path.size()) {
                    path.pop();
                }
                path.top()->right = node;
            }
            path.push(node);
        }
        while (path.size() > 1) {
            path.pop();
        }
        return path.top();
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* recoverFromPreorder(string str) {
        stack<TreeNode*> treeStack;
        TreeNode* root = nullptr;

        int index      = 0;
        int levl       = 0;

        while (index < str.length())
        {
            // 如果是 - ，增加层级
            if (str[index] == '-')
            {
                levl++;
                index++;
                continue;
            }

            // 字符转数字
            int val = 0;
            while (index < str.length() && str[index] != '-')
            {
                val = val * 10 + (str[index] - '0');
                index++;
            }

            // 如果层级低于现在的层级，那么说明它是上某级的右节点
            while (levl < treeStack.size() && treeStack.size() > 0)
            {
                treeStack.pop();
            }

            // 确定节点层级后，要么是根，要么是别人的子节点
            TreeNode* tempNode = new TreeNode(val);
            if (treeStack.size() <= 0)
            {
                root = tempNode;
                treeStack.push(root);
            }     
            //注意看这里！！！
            else if (treeStack.top()->left == NULL)
            {
                treeStack.top()->left = tempNode;
                treeStack.push(treeStack.top()->left);
            }
            //注意看这里！！！
            else if (treeStack.top()->right == NULL)
            {
                treeStack.top()->right = tempNode;
                treeStack.push(treeStack.top()->right);
            }
            
            // 层级清空
            levl = 0;
        }

        return root;
    }
};

最长重复子数组记住，子序列默认不连续，子数组默认连续

注意子数组和子序列的区别如果是子序列的话递推公式就是： dp[i][j] = max(dp[i-1][j-1]+(A[i-1] == B[j-1]?1:0),dp[i-1][j],dp[i][j-1]) 三个里面挑最大

输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出: 3
解释:
长度最长的公共子数组是 [3, 2, 1]。

class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        int n = A.size(), m = B.size();
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                dp[i][j] = A[i-1] == B[j-1] ? dp[i - 1][j - 1] + 1 : 0;
                ans = max(ans, dp[i][j]);
            }
        }
        return ans;
    }
};
------------
class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        int n = A.size(), m = B.size();
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                dp[i+1][j+1] = A[i] == B[j] ? dp[i][j] + 1 : 0;
                ans = max(ans, dp[i+1][j+1]);
            }
        }
        return ans;
    }
};

二叉树C++

#include <iostream>
using namespace std;

typedef struct BinaryTree {
	BinaryTree *Lchild;
	BinaryTree *Rchild;
	int data;
}BinaryTree;
int Construct(BinaryTree **T) {
	int ch;
	cin >> ch;
	if (ch == -1) {
		*T = NULL;
		return 0;
	}
	else
	{
		*T = (BinaryTree *)malloc(sizeof(BinaryTree));
		if (T == NULL)
			cout << "malloc failed!" << endl;
		else
		{
			(*T)->data = ch;
			cout << "请输入" << ch << "的左子节点：" << endl;
			Construct(&((*T)->Lchild));
			Construct(&((*T)->Rchild));
		}
			

	}

}
int main(int argc, char **argv) {
	cout << "BinaryTree Construct Stage..." << endl;
	BinaryTree *Btree;
	cout << "请输入二叉树第一个节点的值，-1代表叶子节点..." << endl;
	Construct(&Btree);
	return 0;
}

BTree本来是一个指向BinaryTree的指针，

因为有小伙伴问了，可否在构建二叉树传入的参数为一级地址。上述的方法是一定要传二级参数的，但是这里给出一个传一级参数的方法，小伙伴也可以通过对比两种方法，对二叉树的构建和传参方式有更深的理解。

struct TreeNode* Create(){
	int val;
	scanf("%d", &val);
	
	struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode*));
	if (val <= 0) {
		return NULL;
	}
	
	if (!root) {
		printf("创建失败\n");
	}
 
	if (val > 0) {
		root->val = val;
		root->left = Create();
		root->right = Create();
	}
	 
	return root;
}

手写：字符串的排列腾讯

class Solution {
public:
    bool checkInclusion(string s1, string s2) {
        int n = s1.length(), m = s2.length();
        if (n > m) {
            return false;
        }
        vector<int> cnt1(26), cnt2(26);
        for (int i = 0; i < n; ++i) {
            ++cnt1[s1[i] - 'a'];
            ++cnt2[s2[i] - 'a'];
        }
        if (cnt1 == cnt2) {
            return true;
        }
        for (int i = n; i < m; ++i) {
            ++cnt2[s2[i] - 'a'];
            --cnt2[s2[i - n] - 'a'];
            if (cnt1 == cnt2) {
                return true;
            }
        }
        return false;
    }
};

手写： rand5实现rand3和rand8

//使用Rand5()实现Rand3()   
int Rand3()  
{  
    int x;  
    do  
    {  
        x = Rand5();  
    } while (x >= 3);  
    return x;  
}  
//利用Rand3编写Rand5怎么办？   
int Rand5()  
{  
    int x;  
    do  
    {  
        x = Rand3() * 3 + Rand3();  
    } while (x >= 5);  
    return x;  
}   
//如果要求利用Rand5编写Rand7怎么办？   
int Rand7()  
{  
    int x;  
    do  
    {  
        x = Rand5() * 5 + Rand5();  
    } while (x >= 21);  
    return x % 7;  
}   
// 这个是[1,10]范围的，所以需要减一
int rand_10()    
{    
    int x = 0;    
    do    
    {    
        x = 7 * (rand7() - 1) + rand7();    
    }while(x > 40);    
    return x % 10 + 1;    
}

手写：判断回文链表

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        if(head == nullptr) return true;
        while(fast->next != nullptr && fast->next->next != nullptr ){
            
            slow = slow->next;
            fast = fast->next->next;
        }
        ListNode* after = slow->next;
        ListNode* prev = NULL;
        while(after != nullptr){
            ListNode* temp = after->next;
            after->next = prev;
            prev = after;
            after = temp;
        }
        
        while(prev != nullptr){
            if(head->val == prev->val){
                head = head->next;
                prev = prev->next;
            }
            else
            return false;
        }       

    return true;
    }
};

寻找旋转排序数组中的最小值

class Solution {
public:
    int findMin(vector<int>& nums) {
        int low = 0;
        int high = nums.size() - 1;
        while (low < high) {
            int pivot = low + (high - low) / 2;
            if (nums[pivot] < nums[high]) {
                high = pivot;
            }
            else {
                low = pivot + 1;
            }
        }
        return nums[low];
    }
};


//        二分查找
        while(low < high){
//            取中间值
            int mid = (high+low)/2;
//            如果中间值小于最大值，则最大值减小
//            疑问：为什么 high = mid;而不是 high = mid-1;
//            解答：{4,5,1,2,3}，如果high=mid-1，则丢失了最小值1
            if (nums[mid] < nums[high]) {
                high = mid;
            } else {
//                如果中间值大于最大值，则最小值变大
//                疑问：为什么 low = mid+1;而不是 low = mid;
//                解答：{4,5,6,1,2,3}，nums[mid]=6，low=mid+1,刚好nums[low]=1
//                继续疑问：上边的解释太牵强了，难道没有可能low=mid+1,正好错过了最小值
//                继续解答：不会错过!!! 如果nums[mid]是最小值的话，则其一定小于nums[high],走if，就不会走else了
                low = mid+1;
            }
        }
//        疑问：为什么while的条件是low<high,而不是low<=high呢
//        解答：low<high，假如最后循环到{*,10,1,*}的这种情况时，nums[low]=10,nums[high]=1,nums[mid]=10,low=mid+1,
//             直接可以跳出循环了,所以low<high,此时low指向的就是最小值的下标;
//             如果low<=high的话，low=high，还会再不必要的循环一次，此时最后一次循环的时候会发生low==high==mid，
//             则nums[mid]==nums[high]，则会走一次else语句，则low=mid+1,此时low指向的是最小值的下一个下标，
//             则需要return[low-1]
        return nums[low];

199周赛

房间中有 n 个灯泡，编号从 0 到 n-1 ，自左向右排成一行。最开始的时候，所有的灯泡都是关着的。

请你设法使得灯泡的开关状态和 target 描述的状态一致，其中 target[i] 等于 1 第 i 个灯泡是开着的，等于 0 意味着第 i 个灯是关着的。

有一个开关可以用于翻转灯泡的状态，翻转操作定义如下：

选择当前配置下的任意一个灯泡（下标为 i ）
翻转下标从 i 到 n-1 的每个灯泡
翻转时，如果灯泡的状态为 0 就变为 1，为 1 就变为 0 。

返回达成 target 描述的状态所需的最少翻转次数。

聪明人一眼就看出这是找规律，可惜我不是聪明人！这道题就是找相邻两个字符不相同的个数，开头如果有0的话需要把开头这些0去除掉。

输入：target = "10111"
输出：3
解释：初始配置 "00000".
从第 3 个灯泡（下标为 2）开始翻转 "00000" -> "00111"
从第 1 个灯泡（下标为 0）开始翻转 "00111" -> "11000"
从第 2 个灯泡（下标为 1）开始翻转 "11000" -> "10111"
至少需要翻转 3 次才能达成 target 描述的状态

 
输入：target = "001011101"
输出：5

class Solution {
public:
    int minFlips(string target) {
        int count = 1;
        int i = 0;
        while(i < target.size() && target[i] == '0'){
            i++;
        }
        if(i == target.size()) return 0;
        for(; i < target.size() - 1; ++i){
            if(target[i] != target[i+1] ){
                count++;
            }
        }
        return count;
    }
};

来看看大佬的做法：

class Solution {
public:
    int minFlips(string target) {
        int cur = 0, ans = 0;
        for(char c : target) {
            int d = c - '0';
            if((d ^ cur) == 1) {//异或就是异性能得1，能生孩子
                cur ^= 1;//相当于做一个反转
                ans++;
            }
        }
        return ans;
    }
};

手写：二叉搜索树和双向链表

class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if(root == nullptr) return nullptr;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
private:
    Node *pre, *head;
    void dfs(Node* cur) {
        if(cur == nullptr) return;
        dfs(cur->left);
        if(pre != nullptr) pre->right = cur;
        else head = cur;
        cur->left = pre;
        pre = cur;
        dfs(cur->right);
    }
};

作者：jyd
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/solution/mian-shi-ti-36-er-cha-sou-suo-shu-yu-shuang-xian-5/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

前序遍历和中序遍历恢复二叉树

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

手写：二叉树最近父节点

class Solution {
public:
    unordered_map<TreeNode*, TreeNode*> fa;
    unordered_map<TreeNode*, bool> vis;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {        
        fa[root] = nullptr;        
        dfs(root);
        while (p != nullptr) {
            vis[p] = true;
            p = fa[p];
        }
        while (q != nullptr) {
            if (vis[q]) return q;
            q = fa[q];
        }
        return nullptr;
        
    }
    void dfs(TreeNode* root) {
        if (root == nullptr) return;
        fa[root->left] = root;
        fa[root->right] = root;
        dfs(root->left);
        dfs(root->right);
    }
};

求一个字符串中连续出现次数最多的子串

例如字符串“abababc”,最多连续出现的为ab，连续出现三次。要和求一个字符串中的最长重复子串区分开来，还是上面的字符串，那么最长的重复子串为abab。两个题目的解法有些类似，都用到了后缀数组这个数据结构。求一个字符串中连续出现的次数最多的子串，首先生成后缀数组例如上面的字符串为:

abababc
bababc
ababc
babc
abc
bc
c

可以看出第一个后缀数组和第三个后缀数组的起始都为ab，第5个后缀数组也为ab。可以看出规律来，一个字符串s，如果第一次出现在后缀数组i的前面，那么如果它重复出现，下一次出现应该在第i+len(s)个后缀数组的前面。

#include <iostream>
#include <cstring>
#include <utility>
#include <string>
#include <vector>
using namespace std;

pair<int, string> fun(const string& str)
{
    vector<string> subs;
    int len = str.size();
    for (int i = 0; i < len; i++)
    {
        subs.push_back(str.substr(i));
    }

    int count = 1;
    int maxCount = 1;
    string sub;

    for (int i = 0; i < len; i++)
    {
        for (int j = i + 1; j < len; j++)
        {
            count = 1;
            if (subs[i].substr(0, j - i) == subs[j].substr(0, j - i))
            {
                ++count;
                //j-i为子串长度
                for (int k = j + j - i; k < len; k += j - i)
                {
                    if (subs[i].substr(0, j - i) == subs[k].substr(0, j - i))
                    {
                        ++count;
                    }
                    else
                    {
                        break;
                    }
                }
                if (count > maxCount)
                {
                    maxCount = count;
                    sub = subs[i].substr(0, j - i);
                }
            }
        }
    }

    return make_pair(maxCount, sub);
}

int main()
{
    string str;
    pair<int, string> rs;
    while (cin>>str)
    {
        rs = fun(str);
        cout<<rs.second<<":"<<rs.first<<endl;
    }

    return 0;
}

手写：删除排序数组中的重复项

i 慢指针，j快指针，当j和i不同时，交换i的下一个元素

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        int i = 0;
        for (int j = 0; j < nums.size(); ++j) {
            if (nums[j] != nums[i]) {
                i++;
                swap(nums[i], nums[j]);                
            }            
        }
        return i + 1;
    }
};

手写：两栈实现队列

class MyQueue {
public:
    /** Initialize your data structure here. */
    MyQueue() {

    }
    
    /** Push element x to the back of queue. */
    void push(int x) {
        A.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        if (B.empty()) {
            while (!A.empty()) {
                B.push(A.top());
                A.pop();
            }
        }
        int ret = B.top();
        B.pop();
        return ret;
    }
    
    /** Get the front element. */
    int peek() {
        int ans = this->pop();
        B.push(ans);
        return ans;
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return A.empty() && B.empty();
    }
private:
    stack<int> A;
    stack<int> B;    
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */

手写：不含有重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

示例 1:

输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(s.size() == 0) return 0;
        unordered_set<char> lookup;
        int maxStr = 0;
        int left = 0;
        for(int i = 0; i < s.size(); i++){
            while (lookup.find(s[i]) != lookup.end()){
                lookup.erase(s[left]);
                left ++;
            }
            maxStr = max(maxStr,i-left+1);
            lookup.insert(s[i]);
    }
        return maxStr;
        
    }
};

手写：最长回文子串

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        string ans;
        for (int l = 0; l < n; ++l) {
            for (int i = 0; i + l < n; ++i) {
                int j = i + l;
                if (l == 0) {
                    dp[i][j] = 1;
                } else if (l == 1) {
                    dp[i][j] = (s[i] == s[j]);
                } else {
                    dp[i][j] = (s[i] == s[j] && dp[i + 1][j - 1]);
                }
                if (dp[i][j] && l + 1 > ans.size()) {
                    ans = s.substr(i, l + 1);
                }
            }
        }
        return ans;
    }
};

手写：反转单词

class Solution {
public:
    string reverseWords(string s) {
        vector<string> str;
        string temp;
        if (s.empty()) return "";

        for (int i = 0; i < s.size(); ++i) {
            if (s[i] != ' ') {
                temp += s[i];
            }
            else if (temp.size() > 0) {
                str.push_back(temp);
                temp.clear();
            }
        }
        str.push_back(temp);
        reverse(str.begin(), str.end());
        string ret;
        for (int i = 0; i < str.size(); ++i) {
            if (str[i].size()) {
                ret += str[i];
                if (i != str.size() - 1)
                    ret += ' ';
            }
        }
        //ret.erase(ret.end() - 1);
        return ret;
    }
};

手写：字符串相加

class Solution {
public:
    string addStrings(string num1, string num2) {
        int i = num1.length() - 1, j = num2.length() - 1, add = 0;
        string ans = "";
        while (i >= 0 || j >= 0 || add != 0) {
            int x = i >= 0 ? num1[i] - '0' : 0;
            int y = j >= 0 ? num2[j] - '0' : 0;
            int result = x + y + add;
            ans.push_back('0' + result % 10);
            add = result / 10;
            i -= 1;
            j -= 1;
        }
        // 计算完以后的答案需要翻转过来
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

手写：两数链表相加

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* head = nullptr;
        ListNode* tail = head;
        int carry = 0;
        while (l1 || l2) {
            int val_1 = l1? l1->val : 0;
            int val_2 = l2? l2->val : 0;
            int sum = val_1 + val_2 + carry;
            carry = sum / 10;
            if (head == nullptr) {
                head = tail = new ListNode(sum % 10);
            }
            else {
                tail->next = new ListNode(sum % 10);
                tail = tail->next;
            }

            if (l1) l1 = l1->next;
            if (l2) l2 = l2->next;
        }
        if (carry) tail->next = new ListNode(carry);
        return head;
    }
};

手写：LRU缓存

## LRU缓存

```c
struct LinkNode {
    int key, value;
    LinkNode* prev;
    LinkNode* next;
    LinkNode() : key(0), value(0), prev(nullptr), next(nullptr) {}
    LinkNode(int _key, int _value) : key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
    unordered_map<int, LinkNode*> cache;
    LinkNode* head;
    LinkNode* tail;
    int size;
    int capacity;
   
public:
    LRUCache(int _capacity) : capacity(_capacity), size(0) {
        head = new LinkNode();
        tail = new LinkNode();
        head->next = tail;
        tail->prev = head;
    }
    
    int get(int key) {
        if (!cache.count(key)) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        LinkNode* node = cache[key];
        moveToHead(node);
        return node->value;
    }
    
    void put(int key, int value) {
        //1\如果key不存在，添加进去
        if (cache.count(key) == 0) {
            LinkNode* node = new LinkNode(key, value);
            cache[key] = node;
            node->next = head->next;
            node->prev = head;
            head->next->prev = node;
            head->next = node;
            ++size;
            if (size > capacity) {
                 LinkNode* tailNode = tail->prev;
                 tailNode->prev->next = tail;
                 tailNode->next->prev = tailNode->prev;
                 cache.erase(tailNode->key);
                 delete tailNode;
                 --size;
            }
        }else{
            LinkNode* node = cache[key];
            node->value = value;
            moveToHead(node);
        }

    }

    void moveToHead(LinkNode* node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
        head->next->prev = node;
        node->next = head->next;
        node->prev = head;   
        head->next = node;     
    }
 

};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */
```
class LRUCache {
private:
    int cap;
    list<pair<int, int>>l;
    unordered_map<int, list<pair<int, int>>::iterator>mp;
public:
    LRUCache(int capacity) {
        cap = capacity;
    }
    
    int get(int key) {
        auto it = mp.find(key);
        if(it == mp.end()){
            return -1;
        }
        auto target_pair_it = it->second;
        pair<int, int>np = {target_pair_it->first, target_pair_it->second};
        l.erase(target_pair_it);
        l.push_front(np);
        mp[key] = l.begin();
        return np.second;
    }
    
    void put(int key, int value) {
        pair<int, int>np = {key, value};
        auto it = mp.find(key);
        if(it == mp.end()){
            l.push_front(np);
            mp[key] = l.begin();
        }else{
            auto target_pair_it = it->second;
            l.erase(target_pair_it);
            l.push_front(np);
            mp[key] = l.begin();
        }
        if(l.size() > cap){
            auto remove_k = l.back().first;
            mp.erase(remove_k);
            l.pop_back();
        }
        

    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

作者：fimm
链接：https://leetcode-cn.com/problems/lru-cache-lcci/solution/c-shuang-xiang-lian-biao-shi-yong-stl-list-by-fimm/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

手写：岛屿数量

class Solution {
private:
    void dfs(vector<vector<char>>& grid, int r, int c) {
        int nr = grid.size();
        int nc = grid[0].size();

        grid[r][c] = '0';
        if (r - 1 >= 0 && grid[r-1][c] == '1') dfs(grid, r - 1, c);
        if (r + 1 < nr && grid[r+1][c] == '1') dfs(grid, r + 1, c);
        if (c - 1 >= 0 && grid[r][c-1] == '1') dfs(grid, r, c - 1);
        if (c + 1 < nc && grid[r][c+1] == '1') dfs(grid, r, c + 1);
    }

public:
    int numIslands(vector<vector<char>>& grid) {
        int nr = grid.size();
        if (!nr) return 0;
        int nc = grid[0].size();

        int num_islands = 0;
        for (int r = 0; r < nr; ++r) {
            for (int c = 0; c < nc; ++c) {
                if (grid[r][c] == '1') {
                    ++num_islands;
                    dfs(grid, r, c);
                }
            }
        }

        return num_islands;
    }
};

作者：LeetCode
链接：https://leetcode-cn.com/problems/number-of-islands/solution/dao-yu-shu-liang-by-leetcode/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

手写：找出数组中出现奇数次的元素(

给定一个含有n个元素的整型数组a，其中只有一个元素出现奇数次，找出这个元素。

因为对于任意一个数k，有k ^ k = 0，k ^ 0 = k，所以将a中所有元素进行异或，那么个数为偶数的元素异或后都变成了0，只留下了个数为奇数的那个元素。

#include <stdio.h>
int FindElementWithOddCount(int* a, int n)
{
	int r = a[0];
	for (int i = 1; i < n; ++i)
	{
		r ^= a[i];
	}
	return r;
}
int main()
{
	int array[] = { 1, 2, 2, 3, 3, 4, 1 };
	int len = sizeof(array) / sizeof(array[0]);
	printf("%d\n", FindElementWithOddCount(array, len));
	getchar();
	return 0;
}

手写：实现strStr、KMP

实现字符串匹配算法

class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.empty())
            return 0;
        
        int i=0,j=0;
        while(haystack[i]!='\0'&&needle[j]!='\0')
        {
            if(haystack[i]==needle[j])
            {
                i++;
                j++;
            }
            else
            {
                i=i-j+1; // i 比 j 长，且移动了 j 个单位，回退到之前的下一个位置需要加一
                j=0;
            }
        }
        if(needle[j]=='\0')
            return i-j;
        
        return -1;
    }
};

作者：Nanase_
链接：https://leetcode-cn.com/problems/implement-strstr/solution/c5chong-jie-fa-ku-han-shu-bfkmpbmsunday-by-2227/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

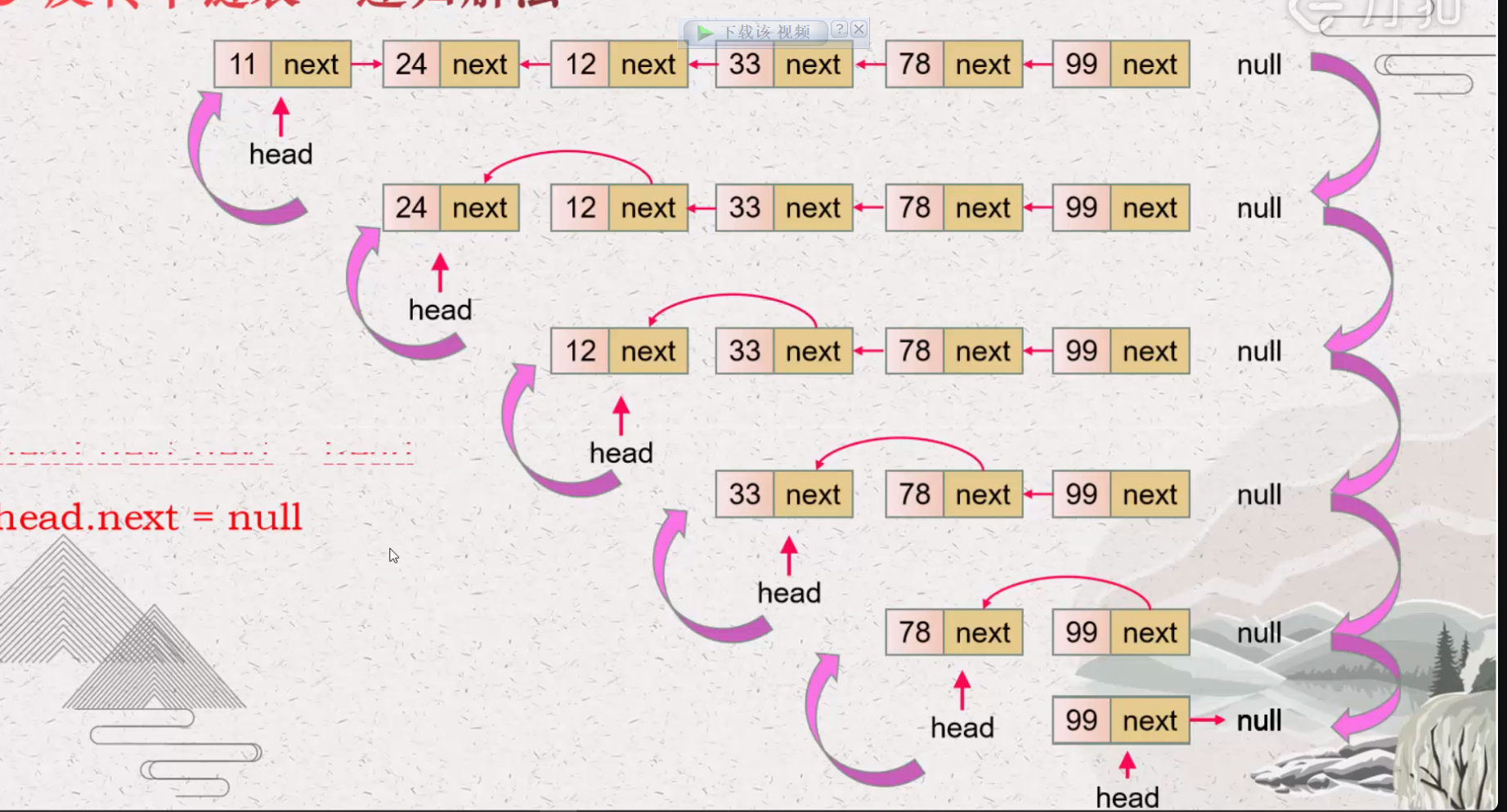
手写：反转链表

注意返回的是 prev 哈！

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == nullptr) return nullptr;
        ListNode* prev = nullptr;
        while (head) {
            ListNode* temp = head->next;
            head->next = prev;            
            prev = head;
            head = temp;
        }
        return prev;
    }
};

递归版本：

public ListNode reverseList(ListNode head) {
    // 1. 递归终止条件
    if (head == null || head.next == null) {
        return head;
    }
    ListNode p = reverseList(head.next);
    head.next.next = head;
    head.next = null;
    return p;
}

手写：反转链表2

反转某段区间内的链表，注意先找到left前一个元素prev_broke，再找到right后一个元素after_broke

反转区间后再连接上，这是我自己写的，特别注意一下区间个数

ListNode* reverseBetween(ListNode* head, int left, int right) {
    if (head == nullptr) return nullptr;
    ListNode* dummyHead = new ListNode(0, head);

    ListNode* prev_broke = dummyHead;
    ListNode* after_broke = dummyHead; // 断开前后节点

    for (int i = 0; i < left - 1; ++i) {
        prev_broke = prev_broke->next;
    }

    for (int i = 0; i <= right; ++i) {
        after_broke = after_broke->next;
    }
    ListNode* prev = nullptr;
    ListNode* tail = prev_broke->next;
    for (int i = left; i <= right; ++i) {
        ListNode* temp = tail->next;
        tail->next = prev;
        prev = tail;
        tail = temp;
    }
    prev_broke->next->next = after_broke;
    prev_broke->next = prev;
    return dummyHead->next;
}

手写：删除链表倒数第 N 个节点

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

示例：

给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.

这道题很巧妙：

其一是设置了一个虚拟的头结点：这是为了防止让你删除倒数第四个结点时结果把自己的头结点给删除了。。。

其二是窗口的大小比你要删除的大小要大一个，这样可以直接用后面那个的next来删除，省却了后面跟一个伴随指针来做删除。所以你看到n+1

注意看它的动图，它最后q指针指向了null，我感到困惑：指到5不就行了吗？

注意他这里是q，而不是q->next。所以指到5之后还要进行一次while循环，因为q不为空嘛！

while(q) 最后一个元素也要参与到运算中 while(q->next)最后一个元素不参与到运算中

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        //ListNode *temp = head;
       ListNode *temp = new ListNode(0);
       temp -> next = head;
       ListNode *last = temp;
       ListNode *first = temp;
        for(int i = 0; i < n+1 ; i++)
        {
            first = first->next;
        }

        while(first)
        {
            last = last->next;
            first = first->next;
        }
			ListNode *delNode = last->next;
			last->next = delNode->next;
			delete delNode;
			
			ListNode *retNode = temp->next;
			delete temp;
			
			return retNode;
        
    }
};

手写：删除链表中重复元素

ListNode* deleteDuplicates(ListNode* head) {
    ListNode* first = head;
    ListNode* second = head;
    while (second) {
        if (first->val != second->val) {
            first = first->next;
            second = second->next;
        }
        else {
            while (second && second->val == first->val) {
                second = second->next;
            }
            first->next = second;
            first = second;
        }
    }
    return head;
}

手写：删除链表中重复元素II

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if (head == nullptr) return nullptr;
        ListNode* dummyHead = new ListNode(0, head);

        ListNode* curr = dummyHead;
        while (curr->next && curr->next->next) {
            if (curr->next->val == curr->next->next->val) {
                int val = curr->next->val;
                while (curr->next && curr->next->val == val) {
                    curr->next = curr->next->next;
                }
            }
            else {
                curr = curr->next;
            }
        }
        return dummyHead->next;
    }
};

手写：环形链表II

判断环形链表入环点

ListNode *detectCycle(ListNode *head) {
     ListNode* slow = head;
     ListNode* fast = head;
     while (fast) {
         slow = slow->next;
         if (fast->next == nullptr) return nullptr;
         fast = fast->next->next;
         if (slow == fast) {
             ListNode* ptr = head;
             while (ptr != slow) {
                 slow = slow->next;
                 ptr = ptr->next;
             }
             return ptr;
         } 
     }
     return nullptr;
 }

手写：最小栈

我这么写太麻烦，不如按照官方题解那样

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {

    }
    
    void push(int x) {
        stk.push(x);
        if (min_stk.empty() || min_stk.top() >= x) min_stk.push(x);       
    }
    
    void pop() {
        if (stk.top() == min_stk.top()) {
            stk.pop();
            min_stk.pop();
        }
        else {
            stk.pop();
        }
    }
    
    int top() {
        return stk.top();
    }
    
    int getMin() {
        return min_stk.top();
    }
private:
    stack<int> stk;
    stack<int> min_stk;    
};

官方题解：

class MinStack {
    stack<int> x_stack;
    stack<int> min_stack;
public:
    MinStack() {
        min_stack.push(INT_MAX);
    }
    
    void push(int x) {
        x_stack.push(x);
        min_stack.push(min(min_stack.top(), x));
    }
    
    void pop() {
        x_stack.pop();
        min_stack.pop();
    }
    
    int top() {
        return x_stack.top();
    }
    
    int getMin() {
        return min_stack.top();
    }
};

注意和窗口最小值和最小队列区分开来，那两个需要无限弹出

如果说只用一个栈的话可以:

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {
    }
    
    void push(int x) {
        if (st.size() == 0) {
            st.push({x, x});
        } else {
            st.push({x, min(x, st.top().second)});
        }
    }
    
    void pop() {
        st.pop();
    }
    
    int top() {
        return st.top().first;
    }
    
    int getMin() {
        return st.top().second;
    }
private:
    stack<pair<int, int>> st;
};

手写：三数之和

注意去重处理：不光第一个元素需要去重，第二个元素也需要去重

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        if (nums.size() < 3) return {};
        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        for (int i = 0; i < nums.size() - 2; ++i) {
            if (nums[i] > 0) continue;
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }       
            int right = nums.size() - 1;
            for (int left = i + 1; left < right; ++left) {
                if (left > i + 1 && nums[left] == nums[left - 1]) {
                    continue;
                }
                while (left < right && nums[left] + nums[right] > -nums[i]) {
                    --right;
                }
                if (left == right) break;
                if (nums[left] + nums[right] == -nums[i]) {
                    res.push_back({nums[i], nums[left], nums[right]});
                }
            }     

        }
        return res;
    }
};
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        int size = nums.size();
        if (size < 3)   return {};          // 特判
        vector<vector<int> >res;            // 保存结果（所有不重复的三元组）
        std::sort(nums.begin(), nums.end());// 排序（默认递增）
        for (int i = 0; i < size; i++)      // 固定第一个数，转化为求两数之和
        {
            if (nums[i] > 0)    return res; // 第一个数大于 0，后面都是递增正数，不可能相加为零了
            // 去重：如果此数已经选取过，跳过
            if (i > 0 && nums[i] == nums[i-1])  continue;
            // 双指针在nums[i]后面的区间中寻找和为0-nums[i]的另外两个数
            int left = i + 1;
            int right = size - 1;
            while (left < right)
            {
                if (nums[left] + nums[right] > -nums[i])
                    right--;    // 两数之和太大，右指针左移
                else if (nums[left] + nums[right] < -nums[i])
                    left++;     // 两数之和太小，左指针右移
                else
                {
                    // 找到一个和为零的三元组，添加到结果中，左右指针内缩，继续寻找
                    res.push_back(vector<int>{nums[i], nums[left], nums[right]});
                    left++;
                    right--;
                    // 去重：第二个数和第三个数也不重复选取
                    // 例如：[-4,1,1,1,2,3,3,3], i=0, left=1, right=5
                    while (left < right && nums[left] == nums[left-1])  left++;
                    while (left < right && nums[right] == nums[right+1])    right--;
                }
            }
        }
        return res;
    }
};

手写：string

class string {
public:
    ~string(){
        if (m_data != NULL) { // 这里忘了判断
            delete[] m_data;
            m_data = NULL;
        }        
    }
    string(const char* s) { // 这块忘了加const
        if (s == NULL) {
            m_data = new char[1];
            *m_data = '\0';
        }
        else {
            int sz = strlen(s);
            m_data = new char[sz + 1];
            strcpy(m_data, s);           
        }
    };
    // 拷贝构造
    string(const string& s) {
        int sz = strlen(s);
        m_data = new char[sz + 1];
        strcpy(m_data, s.m_data);// 这块写错为strcpy(m_data, s);
    }
    string& operator = (const string& s) {
        if (*this == s) 
            return *this;
        delete[] m_data;
        int len = strlen(s.m_data);
        m_data = new char[len + 1];
        strcpy(m_data, s.m_data);
        return *this;
    }
private:
    char* m_data;
}

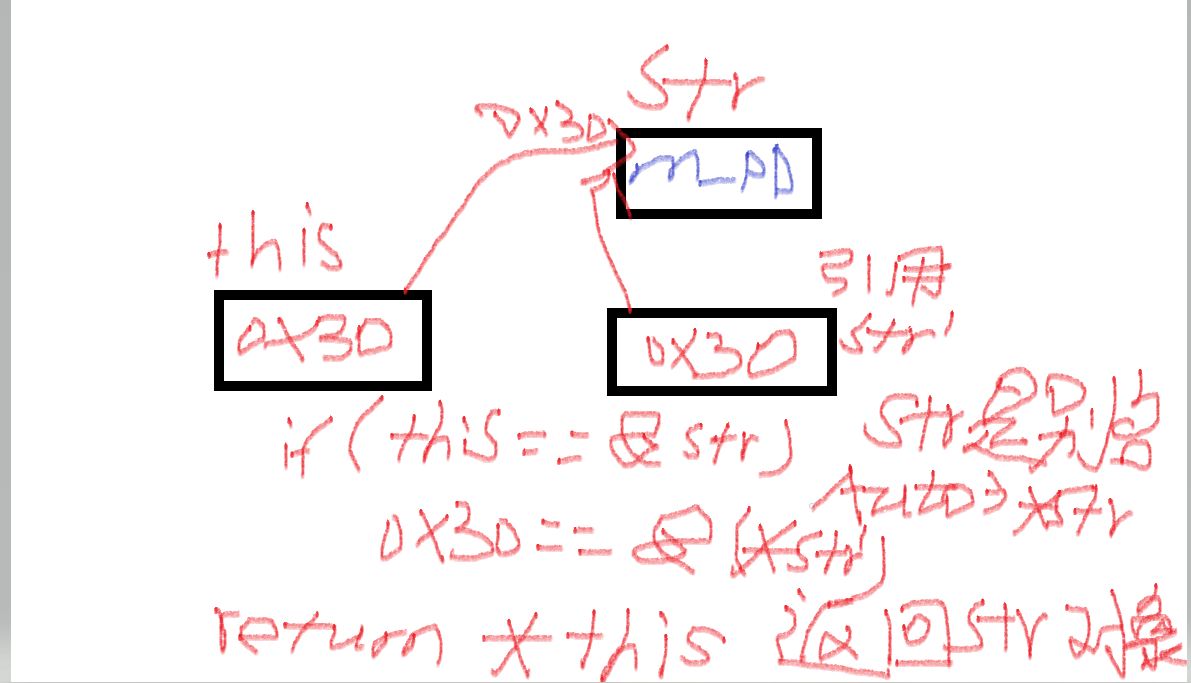
手写：string

class CMyString
{
public:
    CMyString(char* pData = nullptr);
    CMyString(const CMyString& str);
    ~CMyString(void);

    CMyString& operator = (const CMyString& str);

    void Print();
      
private:
    char* m_pData;
};

CMyString::CMyString(char *pData)
{
    if(pData == nullptr)
    {
        m_pData = new char[1];
        m_pData[0] = '\0';
    }
    else
    {
        int length = strlen(pData);
        m_pData = new char[length + 1];
        strcpy(m_pData, pData);
    }
}

CMyString::CMyString(const CMyString &str)
{
    int length = strlen(str.m_pData);
    m_pData = new char[length + 1];
    strcpy(m_pData, str.m_pData);
}

CMyString::~CMyString()
{
    delete[] m_pData;
}

CMyString& CMyString::operator = (const CMyString& str)
{
    if(this == &str)
        return *this;
	cout << this << endl;
	//cout << str << endl;
	cout << &str << endl;
    delete []m_pData;
    m_pData = nullptr;

    m_pData = new char[strlen(str.m_pData) + 1];
    strcpy(m_pData, str.m_pData);

    return *this;
}

手写：线程安全单例模式

在c++设计模式中提出一种很简单的实现方法：其实现过程是这样的，首先要保证一个类只有一个实例，而且使用类静态指针指向唯一的实例；当然就在类中构造一个实例，那么就要调用构造函数，为了防止在类的外部调用类的构造函数创建实例，需要将构造函数访问权限设计成私有的；当然要提供一个全局的访问节点，那么就类中定义一个static函数，在其函数体中调用类的构造函数创建实例并且返回这个唯一的构造实例。说了这么多，还不如上代码仔细品味这段话的意思，代码:

我们从头到尾都没考虑线程安全问题，如果你使用第四种方法，恭喜你无意识中避免了线程安全，这又另外一个话题了：在c++ 11新标准中，静态局部变量是线程安全的参考文章：http://anotherlayer.net/2012/05/04/static-initialization-and-thread-safety/

#include <iostream>
using namespace std;
 
class Singleton
{
public:
	static Singleton* get_instance()
	{
		static Singleton instance;
		return &instance;
	}
 
private:
	Singleton(){}; //构造函数设计成私有的
 
	Singleton(const Singleton&);
 
	Singleton& operator==(const Singleton&);
 
};
 
int main(int argc, char*argv[])
{
	Singleton *object = Singleton::get_instance();
 
	return 0;
}

class singleton {
private:
    singleton() {}
    static singleton *p;
public:
    static singleton *instance();
};

singleton *singleton::p = new singleton();
singleton* singleton::instance() {
    return p;
}

手写：智能指针

// this 是对象的地址，that 是一个引用，会被自动解引用为 * that,所以为了获取对象地址，需要使用&取地址

if (this != &that)

或者还可以写成 if (*this == that)

#pragma once

template<class T>
class SharedPointer
{
public:
	//默认构造函数，内部指针，未指向任何资源，引用计数为0,因为它未与任何资源绑定
	SharedPointer() :m_refCount(nullptr), m_pointer(nullptr) {}

	//构造函数，初始化时，指向一个已经分配好的资源
	SharedPointer(T* adoptTarget) :m_refCount(nullptr), m_pointer(adoptTarget)
	{
		addReference();
	}

	//构造函数，使用其它对象创建新对象
	SharedPointer(const SharedPointer<T>& copy)
		:m_refCount(copy.m_refCount), m_pointer(copy.m_pointer)
	{
		addReference();
	}

	//析构函数，引用计数递减，当为0时，释放资源
	virtual ~SharedPointer()
	{
		removeReference();
	}

	//赋值操作
	//当左值被赋值时，表明它不再指向所指的资源，故引用计数减一
	//之后，它指向了新的资源，所以对应这个资源的引用计数加一
	SharedPointer<T>& operator=(const SharedPointer<T>& that)
	{
        // this 是对象的地址，that 是一个引用，会被自动解引用为 * that,所以为了获取对象地址，需要使用&取地址
		if (this != &that)
		{
			removeReference();
			this->m_pointer = that.m_pointer;
			this->m_refCount = that.m_refCount;
			addReference();
		}
		return *this;
	}

	//判断是否指向同一个资源
	bool operator==(const SharedPointer<T>& other)
	{
		return m_pointer == other.m_pointer;
	}
	bool operator!=(const SharedPointer<T>& other)
	{
		return !operator==(other);
	}

	//指针解引用
	T& operator*() const
	{
		return *m_pointer;
	}
	//调用所知对象的公共成员
	T* operator->() const
	{
		return m_pointer;
	}

	//获取引用计数个数
	int GetReferenceCount() const
	{
		if (m_refCount)
		{
			return *m_refCount;
		}
		else
		{
			return -1;
		}
	}

protected:
	//当为nullpter时，创建引用计数资源，并初始化为1
	//否则，引用计数加1。
	void addReference()
	{
		if (m_refCount)
		{
			(*m_refCount)++;
		}
		else
		{
			m_refCount = new int(0);
			*m_refCount = 1;
		}
	}

	//引用计数减一，当变为0时，释放所有资源
	void removeReference()
	{
		if (m_refCount)
		{
			(*m_refCount)--;
			if (*m_refCount == 0)
			{
				delete m_refCount;
				delete m_pointer;
				m_refCount = 0;
				m_pointer = 0;
			}
		}
	}

private:
	int* m_refCount;
	T* m_pointer;
};

举个例子，遍历经过 IVIV 的时候先记录 II 的对应值 11 再往前移动一步记录 IVIV 的值 33，加起来正好是 IVIV 的真实值 44。max 函数在这里是为了防止遍历第一个字符的时候出现 [-1:0]的情况

class Solution {
public:
    int romanToInt(string s) {
        unordered_map<string, int> m = {{"I", 1}, {"IV", 3}, {"IX", 8}, {"V", 5}, {"X", 10}, {"XL", 30}, {"XC", 80}, {"L", 50}, {"C", 100}, {"CD", 300}, {"CM", 800}, {"D", 500}, {"M", 1000}};
        int r = m[s.substr(0, 1)];
        for(int i=1; i<s.size(); ++i){
            string two = s.substr(i-1, 2);
            string one = s.substr(i, 1);
            r += m[two] ? m[two] : m[one];
        }
        return r;
    }
};

手写：旋转链表

给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL

class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
    if (head == NULL) return NULL;
    if (head->next == NULL) return head;
    ListNode* temp;
    temp = head;
    int length = 1;

        while (temp->next)
        {
            ++length;
            temp = temp->next;
        }
        temp->next = head;
        if (k%=length)
        {
            for (int i = 0; i < length - k; ++i)
            {
                temp = temp->next;
            }
        }
        ListNode* res = temp->next;
        temp->next = NULL;
    return res;
    }
};

这个代码有以下几个值得学习的地方：

将链表做成一个回环：注意空链表与单链表特例

使用++len而不是len++，省却拷贝花销

这里的k%=len很巧妙：其一是对于0和链表长度的k不进行处理–因为就算翻转过来也和原链表一样

其二是将k值重新设置为小于等于len的数值，防止下面len-k出现溢出

还有一点需要注意的是每次你想设置一个节点来追踪前链表元素的时候，不妨考虑一下少走一步？

我本来for循环里是写的head= head->next，前面设置一个节点来做游标，不如人家这个直接使用temp尾节点来做游标好一些。。。

手写：strcpy()

#include<iostream>
using namespace std;

char* strcpy(char *strSrc, char *strDest)
{
	if ((strSrc == NULL) || (strDest == NULL))
		return NULL;
	char *strDestCopy = strDest;
	while ((*strDest++ = *strSrc++) != '\0');
		return strDestCopy;
}


int main()
{
	char strSrc[] = "Hello World!";
	char strDest[20];
	strcpy(strSrc, strDest);
	cout << "strDest: " << strDest << endl;
	return 0;
}

手写：链表相邻元素翻转

输入 bacd 输出 abdc

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* temp = dummyHead;
        while (temp->next != nullptr && temp->next->next != nullptr) {
            ListNode* node1 = temp->next;
            ListNode* node2 = temp->next->next;
            temp->next = node2;
            node1->next = node2->next;
            node2->next = node1;
            temp = node1;
        }
        return dummyHead->next;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/swap-nodes-in-pairs/solution/liang-liang-jiao-huan-lian-biao-zhong-de-jie-di-91/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

手写：K 个一组翻转链表

class Solution {
public:
    // 翻转一个子链表，并且返回新的头与尾
    pair<ListNode*, ListNode*> myReverse(ListNode* head, ListNode* tail) {
        ListNode* prev = tail->next;
        ListNode* p = head;
        while (prev != tail) {
            ListNode* nex = p->next;
            p->next = prev;
            prev = p;
            p = nex;
        }
        return {tail, head};
    }

    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* hair = new ListNode(0);
        hair->next = head;
        ListNode* pre = hair;

        while (head) {
            ListNode* tail = pre;
            // 查看剩余部分长度是否大于等于 k
            for (int i = 0; i < k; ++i) {
                tail = tail->next;
                if (!tail) {
                    return hair->next;
                }
            }
            ListNode* nex = tail->next;
            // 这里是 C++17 的写法，也可以写成
            // pair<ListNode*, ListNode*> result = myReverse(head, tail);
            // head = result.first;
            // tail = result.second;
            tie(head, tail) = myReverse(head, tail);
            // 把子链表重新接回原链表
            pre->next = head;
            tail->next = nex;
            pre = tail;
            head = tail->next;
        }

        return hair->next;
    }
};

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    pair<ListNode*, ListNode*> myReverse(ListNode* head, ListNode* tail) {
        ListNode* prev = nullptr;
        ListNode* p = head;
        while (prev != tail) {
            ListNode* nex = p->next;
            p->next = prev;
            prev = p;
            p = nex;
        }
        return {head, tail};
    }
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* prev = dummyHead;
        while (head) {
            ListNode* tail = prev;
            for (int i = 0; i < k; ++i) {                
                tail = tail->next;
                if (tail == nullptr) return dummyHead->next;
            }
            ListNode* nex = tail->next;
            pair<ListNode*, ListNode*> result = myReverse(head, tail);
            
            head = result.first;
            tail = result.second;
            // cout << prev->val << " " << head->val << endl;
            prev->next = tail;
            head->next = nex;
            prev = head;
            head = nex;
            // cout << prev->val << " " << head->val << endl;
        }
        return dummyHead->next;
    }
};

手写：合并两个有序链表

ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
    if ((!a) || (!b)) return a ? a : b;
    ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
    while (aPtr && bPtr) {
        if (aPtr->val < bPtr->val) {
            tail->next = aPtr; aPtr = aPtr->next;
        } else {
            tail->next = bPtr; bPtr = bPtr->next;
        }
        tail = tail->next;
    }
    tail->next = (aPtr ? aPtr : bPtr);
    return head.next;
}

手写：统计数组中不同元素出现的次数

（时间复杂度O(n)，空间复杂度O(1))

vector findNumbers(vector& nums) {
        int n = nums.size();
        for (int i = 0; i < n; ++ i )
        {
            while (nums[i] > 0)
            {
                int cur;
                if (nums[nums[i]-1] > 0) 
                {
                    cur = nums[i]-1;
                    nums[i] = nums[nums[i]-1];
                    nums[cur] = -1;
                }
                else if (nums[nums[i]-1] != inf)
                {
                    cur = nums[i]-1;
                    nums[i] = inf;
                    nums[cur] -= 1;
                }
                else
                {
                    cur = nums[i]-1;
                    nums[i] = inf;
                    nums[cur] = -1;
                }
            }
        }
        vector ans;
        for (int i = 0; i < n; ++ i ) 
            if (nums[i] == inf) ans.push_back(0);
            else ans.push_back(-nums[i]);
        return ans;
    }
-------------------------------
#include <iostream> 
#include <algorithm> 
#include <vector> 
#include <queue>
#include <stack>
#include <string> 
#include <string.h> 
#include <fstream> 
#include <map> 
#include <iomanip> 
#include <cstdio> 
#include <cstdlib>
#include <cmath>
#include <deque>
#include <hash_map>
 
using namespace std; 
 
const int MAX = 0x7FFFFFFF; 
const int MIN = 0x80000000; 
 
void work(int a[], int n)
{
	int i = 0;
	while(i < n)
	{
		int temp = a[i] - 1;
		if(temp < 0)
		{
			i++;
			continue;
		}
		if(a[temp] > 0)
		{
			a[i] = a[temp];
			a[temp] = -1;
		}
		else
		{
			a[temp]--;
			a[i] = 0;
		}
	}
}
 
int main()
{
	int n;
	while(cin >> n)
	{
		int *a = new int[n];
		for(int i = 0; i < n; i++)
			cin >> a[i];
		work(a, n);
		for(int i = 0; i < n; i++)
			if(a[i] < 0)
				cout << i + 1 << " " << (-a[i]) << endl;
		cout << "********************" << endl;
		delete[] a;
	}
	system("pause");
	return 0;
}

手写：统计一个数字在排序数组中出现的次数

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2
示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

class Solution {
    public int search(int[] nums, int target) {
        // 搜索右边界 right
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= target) i = m + 1;
            else j = m - 1;
        }
        int right = i;
        // 若数组中无 target ，则提前返回
        if(j >= 0 && nums[j] != target) return 0;
        // 搜索左边界 right
        i = 0; j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] < target) i = m + 1;
            else j = m - 1;
        }
        int left = j;
        return right - left - 1;
    }
}

作者：jyd
链接：https://leetcode-cn.com/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/solution/mian-shi-ti-53-i-zai-pai-xu-shu-zu-zhong-cha-zha-5/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

牛客：字符串压缩

#include <iostream>
using namespace std;
int main(int argc, char** argv) {
    string s;
    cin >> s;
    int i = 0;
    while (i < strlen(s)) {
        if (s[i] == ']') {
            int j = i; // j 用来向前寻找 [
            int k = i; // k 用来向前寻找 |
            while (s[j] != '[') {
                if (s[j] == '|') {
                    k = j;
                }
                --j;
            }
            int len = stoi(s.substr(j + 1, k - j - 1));
            string s1 = s.substr(k + 1, i - k - 1); // s1 存储 | 之后的字符串
            string s2;
            for (int p = 0; p < len; ++p) {
                s2 += s1;
            }
            s.replace(j, i - j + 1, s2);
            i = j;
        }
        ++i;
    }
    cout << s;
}

手写：string to int

class Solution {
public:
    int strToInt(string str) {
        int i = 0, flag = 1;
        long res = 0; //默认flag = 1，正数
        while (str[i] == ' ') i ++;
        if (str[i] == '-') flag = -1;
        if (str[i] == '-' || str[i] == '+') i ++;
        for (; i < str.size(); i++)  {
            if(str[i]<'0'||str[i]>'9') break;
            res = res * 10 + (str[i] - '0');
            if (res >= INT_MAX && flag == 1) return  INT_MAX;
            if (res > INT_MAX && flag == -1) return  INT_MIN;
        } 
        return flag * res;
    }
};

字符匹配

题目：glob是一种Unix风格的路径匹配模式，其规则如下：
1.字符/作为分隔符存在
2.字符*匹配除/之外的任意长度的任意字符
3.字符？匹配除/之外的单个长度的任意字符
4.中括号[]用来转移‘*’、‘？’、‘[‘、’]‘这四个特殊字符，一次转义一个字符
5.其他字符保持原有含义
6.对’.‘号开头的文件夹或者文件名，规则1，2不生效
输入1：“pattern. *”,”pattern.txt”
输出1：true

输入2：“dir/*”,”dir/.env”
输出2：false

手写：二分法

二分法第一种写法

以这道题目来举例，以下的代码中定义 target 是在一个在左闭右闭的区间里，「也就是[left, right] （这个很重要）」。

这就决定了这个二分法的代码如何去写，大家看如下代码：

「大家要仔细看注释，思考为什么要写while(left <= right)，为什么要写right = middle - 1」。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n - 1; // 定义target在左闭右闭的区间里，[left, right] 
        while (left <= right) { // 当left==right，区间[left, right]依然有效
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle;
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前  [0, -1]
        // 目标值等于数组中某一个元素  return middle;
        // 目标值插入数组中的位置 [left, right]，return  right + 1
        // 目标值在数组所有元素之后的情况 [left, right]， return right + 1
        return right + 1;
    }
};

二分法第一种写法

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) 。

那么二分法的边界处理方式则截然不同。

不变量是[left, right)的区间，如下代码可以看出是如何在循环中坚持不变量的。

「大家要仔细看注释，思考为什么要写while (left < right)，为什么要写right = middle」。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n; // 定义target在左闭右开的区间里，[left, right)  target
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在 [middle+1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值的情况，直接返回下标
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前 [0,0)
        // 目标值等于数组中某一个元素 return middle
        // 目标值插入数组中的位置 [left, right) ，return right 即可
        // 目标值在数组所有元素之后的情况 [left, right)，return right 即可
        return right;
    }
};

0303

查找旋转排序数组的最小值

注意看当 numbers[pivot] < numbers[high] 时是不减一的哈，因为 pivot 此时可能正在最小值处

        int low = 0;
        int high = numbers.size() - 1;
        while (low <= high) {
            int pivot = low + (high - low) / 2;
            if (numbers[pivot] < numbers[high]) {
                high = pivot;
            }
            else if (numbers[pivot] > numbers[high]) {
                low = pivot + 1;
            }
            else {
                high -= 1;
            }
        }
        return numbers[low];

图片链接：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/solution/xun-zhao-xuan-zhuan-pai-xu-shu-zu-zhong-de-zui--16/

旋转数组的查找特定数字

下面的这个nums[0] <= target 处为何加个 = ？

因为当 nums[0] == target 时，应该让远处的 right 滚回来。而不是让就在此处的 left 再移动了

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = (int)nums.size();
        if (!n) {
            return -1;
        }
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) return mid;
            if (nums[0] <= nums[mid]) {
                if (nums[0] <= target && target < nums[mid]) {
                    r = mid - 1;
                } else {
                    l = mid + 1;
                }
            } else {
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/search-in-rotated-sorted-array/solution/sou-suo-xuan-zhuan-pai-xu-shu-zu-by-leetcode-solut/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

if else

#include <iostream>
 
int main() {
    // 带 else 子句的简单 if 语句
    int i = 5;
    if (i < 2) {
        std::cout << i << " < 2\n";
    } else if(i > 3)
    
    {
        std::cout << i << " > 3\n";
    }
    else if(i > 4){
        std::cout << i << " > 4\n";
    }
}
---------
    5 > 3
--------
//它不执行下面那个 5 > 4 了！！！

if (条件1)
{
    //语句1
}

if (条件2)
{
    //语句2
}

这种格式中，程序会依次判断条件1和条件2是否成立并根据结果决定是否执行语句1和语句2，也就是说，第一个 if 块和第二个 if 块没有影响（除非在执行第一个 if 块的时候就凶残地 return 了）

而下面这种格式，

if (条件1) 
{
    //语句1
}
else if (条件2)
{
    //语句2
}

if 块和 else if 块本质上是互斥的！也就是说，一旦语句1得到了执行，程序会跳过 else if 块，else if 块中的判断语句以及语句2一定会被跳过；同时语句2的执行也暗含了条件1判断失败和语句1没有执行；当然还有第3个情况，就是条件1和条件2都判断失败，语句1和语句2都没有得到执行。

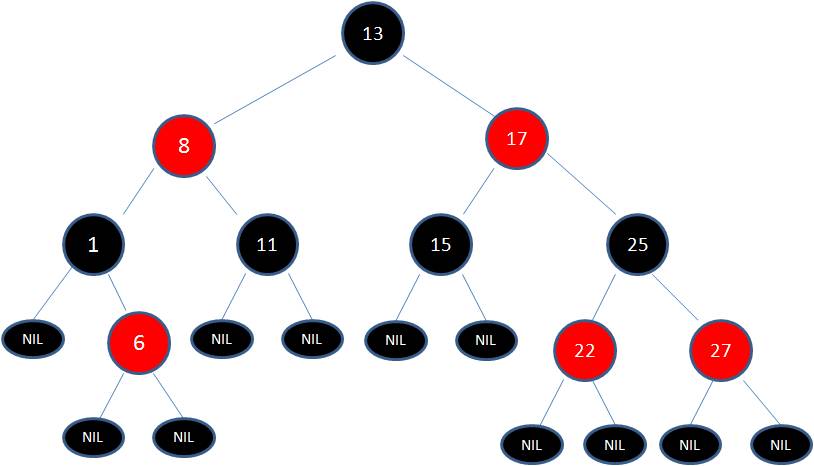
红黑树

1、根节点是黑色；（头头是黑社会）

2、叶子节点（NIL）也是黑色；（小弟也是黑社会）

3、每个红色节点的两个子节点是黑色；（红社会下罩着两个黑社会）

4、从任一节点到其每个叶子的所有路径包含相同数目的黑色节点；（黑社会要均衡，这保证了从根到叶子的最长路径不会超过最短路径的2倍）

0604

今天和7楼另外一个去阿里的学长交流了一下，他拿了阿里腾讯的sp，华为的ssp

1、Linux多线程编程 muduo库 10元（已出）
2、Unix环境高级编程 10元（已出）
3、Unnix网络编程卷一+卷二两本一共15元
4、C++ Primer 15元（已出）
5、Tcp/Ip详解 + Tcp/Ip网际互联两本一共12元（已出）

这几本书研一研二就应该看完

程序员自我修养 Effective C++ + more effective C++ 两本这几本书应该在找工作前看三遍以上，剑指offer 也是，面试时这些C++ 的基础并不会问的很深，但是这几本书会问的很深

美团0313笔试

滑动窗口找最小

#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
#include<unordered_map>
using namespace std;
#define LOCAL
#pragma warning (disable: 4996)
bool comp(pair<int, int> a, pair<int, int> b) {
	return a.second < b.second;
}
int main()
{
	int num, cnt;
#ifdef LOCAL
	freopen("out.txt", "r", stdin);
	//freopen("out.txt", "w", stdout);
#endif
	while (cin >> num >> cnt) {
		vector<int> arr(num);
		for (int i = 0; i < num; ++i) {
			cin >> arr[i];
		}
		for (int i = 0; i < num - cnt + 1; ++i) {
			unordered_map<int, int> hash_;
			vector<pair<int, int>> vec;
			for (int j = 0; j < cnt; ++j) {
				hash_[arr[i + j]]++;
			}
			for (auto& i : hash_) {
				vec.push_back(i);
			}
			std::sort(vec.begin(), vec.end(), [](pair<int, int>& A, pair<int, int>& B) {return A.second > B.second; });
			// for (auto& i : vec) cout << i.first << " :" << i.second << endl;
			if (vec[0].second == 1) {
				std::sort(vec.begin(), vec.end(), [](pair<int, int>& A, pair<int, int>& B) {return A.first < B.first; });
				cout << vec[0].first << endl;
			}
			else 
				cout << vec[0].first << endl;
		}
	}
	return 0;
}

还有一种堆的算法：

//对于基础类型 默认是大顶堆
priority_queue<int> a; 
//等同于 priority_queue<int, vector<int>, less<int> > a;

//             这里一定要有空格，不然成了右移运算符↓
priority_queue<int, vector<int>, greater<int> > c;  //这样就是小顶堆

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main() 
{
    priority_queue<pair<int, int> > a;
    pair<int, int> b(1, 2);
    pair<int, int> c(1, 3);
    pair<int, int> d(2, 5);
    a.push(d);
    a.push(c);
    a.push(b);
    while (!a.empty()) 
    {
        cout << a.top().first << ' ' << a.top().second << '\n';
        a.pop();
    }
}

具体涉及算法如下：

200.岛屿的数量

排列类问题

组合类问题

手写：子集

从先序遍历还原二叉树

最长重复子数组记住，子序列默认不连续，子数组默认连续

二叉树C++

手写：字符串的排列 腾讯

手写： rand5实现rand3和rand8

手写：判断回文链表

寻找旋转排序数组中的最小值

手写：二叉搜索树和双向链表

前序遍历和中序遍历恢复二叉树

手写：二叉树最近父节点

求一个字符串中连续出现次数最多的子串

手写：删除排序数组中的重复项

手写：两栈实现队列

手写：不含有重复字符的最长子串

手写：最长回文子串

手写：反转单词

手写：字符串相加

手写：两数链表相加

手写：LRU缓存

手写：岛屿数量

手写：找出数组中出现奇数次的元素(

手写：实现strStr、KMP

手写：反转链表

手写：反转链表2

手写：删除链表倒数第 N 个节点

手写：删除链表中重复元素

手写：删除链表中重复元素II

手写：环形链表II

手写：最小栈

手写：三数之和

手写：string

手写：string

手写：线程安全单例模式

手写：智能指针

手写：旋转链表

手写：strcpy()

手写：链表相邻元素翻转

手写：K 个一组翻转链表

手写：合并两个有序链表

手写：统计数组中不同元素出现的次数

手写：统计一个数字在排序数组中出现的次数

牛客：字符串压缩

手写：string to int

字符匹配

手写：二分法

if else

红黑树

0604

美团0313笔试

手写：字符串的排列腾讯